小记概率论里的一些题

为了回答这个问题，可以直接考虑不同小孩数量的概率。假设每次生育时，生出女孩的概率为$p$，生出男孩的概率为$q :=1-p$。那么，在这题里：

• 样本空间中的样本点 $\omega_i$ 是长度为 i 的已被生下来的小孩的性别序列。例如，$w_2 = BG$ 表示一共生了两个小孩，第一个是男孩，第二个是女孩；
• 我们设定一个随机变量 $\text{X}(\omega): \Omega \rightarrow \mathbb R$ 。这个随机变量需要输入一个样本点，即上文提到的性别序列，并输出所输入序列的长度值；
• 概率测度 $\text P(x) = \text P(\text{X}=x)$表示「这对夫妻停止生育时，他们已生下的小孩有 x 个」的概率。

不难求出以下递归形式， $$ \begin{align} \text P(1)&=0 \\ \text P(2)&=0 \\ \text P(3)&=p^3 \\ \text P(4)&=qp^3=q\text P(3) \\ \text P(5)&=q^2\text P(3)+qp\text P(3)=q\text P(4)+qp\text P(3) \\ \text P(6)&=q\text P(5)+qp\text P(4)+qp^2\text P(3) \\ \cdots \\ \text P(n)&=q\text P(n-1)+qp\text P(n-2)+qp^2\text P(n-3) \end{align} $$

取$p=0.5$，可得：

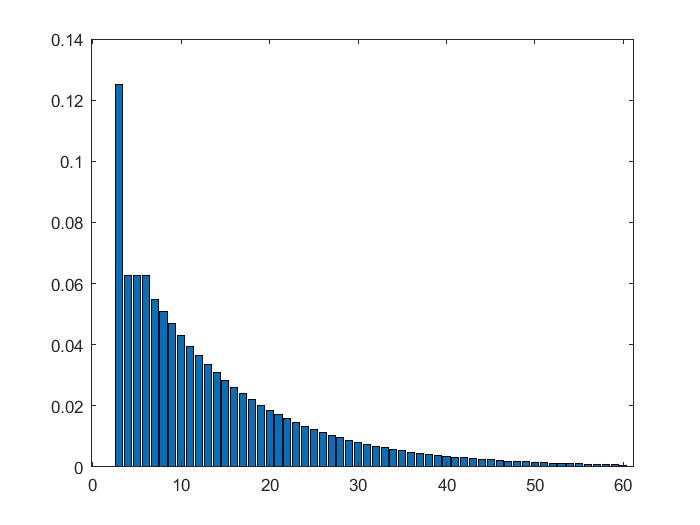
p=0.5; 
q=1-p; 
f=zeros(60,1); 
f(3)=p^3; 
for i=4:60 
    f(i)=q*f(i-1)+q*p*f(i-2)+q*p^2*f(i-3); 
end 
bar(f)

随着k取值的增加，以上表达式中的比值会经历大于1（可能还会等于1）以及小于1的变化。我们希望找到能让上式小于1（即$\frac{p}{1-p} \cdot \frac{n-k}{k+1}<1$）的最小的k。易得： $$ n p-k p<k-k p+1-p \Longleftrightarrow k>p \cdot(n+1)-1 $$

最后可得$k =\lfloor p \cdot(n+1)\rfloor$。

这题一共两问。第一问要求证明题中构造的随机变量$Y$的分布函数与目标分布的函数相等，即$F_Y=F_{服从目标分布的随机变量}$。第二问要求用第一问的结论，构造一个服从几何分布的随机变量。第一小问只需直接计算$Y$的分布函数即可得证。这里只做第二小问。

1. 计算 $X=U_1U_3$ 的分布函数 $$ \begin{aligned} F_{U_1 \cdot U_3}(x) & =P\left(U_1 \cdot U_3 \leq x\right)=\iint_{u_1 \cdot u_3 \leq x} f_{U_1, U_3}\left(u_1, u_3\right) d u_1 d u_3 \\ & =\iint_{u_1 \cdot u_3 \leq x} f_{U_1}\left(u_1\right) \cdot f_{U_3}\left(u_3\right) d u_1 d u_3 \\ & =\int_0^x \int_0^1 d u_3 d u_1+\int_x^1 \int_0^{\frac{x}{u_1}} d u_3 d u_1=\int_0^x d u_1+\int_x^1 \frac{x}{u_1} d u_1 \\ & =x+\left.x \cdot \ln u_1\right|_x ^1=x+x \cdot(0-\ln x) \\ & =x-x \ln x . \end{aligned} $$

2. 使用上一部分求出的分布函数求解 $P[U_1U_3 \leq \frac {U^2_2}{4} ]$ $$ \begin{aligned} P\left(X \leq \frac{U_2^2}{4}\right) & =\iint_{x \leq \frac{u_2^2}{4}} f_{X, U_2}\left(x, u_2\right) d x d u_2=\iint_{x \leq \frac{u_2^2}{4}} f_X(x) \cdot f_{U_2}\left(u_2\right) d x d u_2 \\ & =\int_0^1\left(\int_0^{\frac{u_2^2}{4}}-\ln x \cdot 1 d x\right) d u_2=\int_0^1-\left.(x \cdot(\ln x-1))\right|_0 ^{\frac{u_2^2}{4}} d u_2 \\ & =\int_0^1 \frac{u_2^2}{4} \cdot\left(1-\ln \left(\frac{u_2^2}{4}\right)\right) d u_2=\left|\begin{array}{ll} u=\ln \left(\frac{u_2^2}{4}\right) & d v=\frac{u_2^2}{4} d u_2 \\ d u=\frac{2}{u_2} d u_2 & v=\frac{u_2^3}{12} \end{array}\right| \\ & =\left.\frac{u_2^3}{12}\right|_0 ^1-\left.\frac{u_2^3}{12} \cdot \ln \left(\frac{u_2^2}{4}\right)\right|_0 ^1+\int_0^1 \frac{u_2^2}{6} d u_2=\frac{1}{12}-\frac{1}{12} \cdot \ln \left(\frac{1}{4}\right)+\left.\frac{u_2^3}{18}\right|_0 ^1 \\ & =\frac{1}{12}+\frac{1}{12} \cdot \ln 4+\frac{1}{18} \\ & =\frac{5+3 \cdot \ln 4}{36} . \end{aligned} $$