事件域——划分的精细程度代表所知信息的多寡
简单来说,sigma 代数刻画的事件域 $\mathcal F$ 包含了一系列划分后的集合,后文称作「分类」,which 可以被我们用来对样本空间 $\Omega$ 中的样本路径 $\omega$ 进行归类。这些分类,实际上表示我们对于当前样本路径的了解程度:我们在某一阶段 $T$ 所知道的信息越多,这一阶段的事件域 $\mathcal F _T$ 所包含的元素就越多,表示我们 $\omega$ 所能采用的分类也就越多。
这些分类是怎样描述「所知道的信息」的?一种可行的思路是思路是,对于某个随机过程,我们会面临一条事前确定的样本路径 $\omega_i$ 。然而,尽管这条样本路径是已经被「固定」的,但我们并不知道 $\omega_i$ 是 $\Omega$ 中的哪一个 $\omega$ ——我们仅能知道,对于给定的 $\Omega$ 的某个子集,$\omega_i$ 是不是在这个子集里面。而前一句中 能够被判断是否包含 $\omega_i$ 的这些 $\Omega$ 的子集,就是我们在第一段中提到的,事件域 $\mathcal F$ 所包含的「分类」。如果对集合的划分越精细,「分类」就越多,表示我们知道的信息就更多。
一个例子
对于分类如何刻画信息,现在就来举个直观的例子。假设我现在要扔一枚质地均匀的硬币,扔个 2 次。将硬币的某一面记作正面,与其相反的一面记作反面。将「硬币投出了正面」记作 H (假设其可能性为 $p,p>0$ ),将「硬币投出了反面」记作 T (假设其可能性为 0">$q, q=1-p>0$ )。以一串序列 $\omega$ (其中 $\omega=\omega_1\omega_2$ , 的可能取值为或$\omega_i的可能取值为H或T$ )列出所有可能发生的结果,便可得样本空间 $\Omega = \lbrace \text{HH, HT, TH, TT}\rbrace.$
再定义一个随机变量 $S$ ,用于表示股票价格:
$$ \begin{align} S_0(\omega) &= 4, \forall \omega \in \Omega \\ S_1(\omega) &= \begin{cases} 8, & 如果 \omega_1=H \ 2, & 如果 \omega_1=T \ \end{cases} \\ S_2(\omega) &= \begin{cases} 16, & 如果 \omega_1=\omega_2=H \ 4, & 如果 \omega_1\neq \omega_2 \ 1, & 如果 \omega_1=\omega_2=T \end{cases} \end{align} $$
接下来,假设我们只能观察到 $S(\omega)$ ,而不能直接看到 $\omega$ 是什么。那么接下来,我们便可以用 $\mathcal F$ 刻画该随机过程中所有的信息了。
- 首先是没扔硬币的时候。此时,$\mathcal{F_0} = \lbrace \varnothing, \Omega \rbrace 。$ 这个不难理解。对于给出的一个 $S_0(\omega)$ 的取值,如果该取值不是 4,那说明我们现在不在掷硬币 2 次的这个路径。反之,我们可以推断,我们马上就要开始扔硬币了。此时,我们所知道的信息是:我们是否处于 $\omega$ 的某一可能路径上。
- 接着,是扔 1 次硬币。此时, $S_1(\omega)$的合理取值是 2 或 8 ,对应的事件域是 。$\mathcal{F_1} = \lbrace \varnothing, \Omega, \lbrace HH,HT \rbrace, \lbrace TH,TT \rbrace \rbrace 。$ 这个事件域的含义是,对于观测到的 $S_1(\omega)$ 的取值,我们除了知道「 $S(\omega)$ 对应的 $\omega$ 是否在 $\varnothing 或 \Omega$ 」以外,还能知道 $\omega$ 是哪个值( 还是 $H 还是T?$ )开头的样本路径,即 $\omega$ 到底是属于 $\lbrace HH,HT \rbrace$ ,还是属于 $\lbrace HH,HT \rbrace$ 。
- 最后,是扔第 2 次硬币: $$\begin{equation} \mathcal{F_2} = \lbrace \ \varnothing, \Omega, \ \lbrace \text{HH}\rbrace,\lbrace \text{HT}\rbrace,\lbrace \text{TH}\rbrace, \lbrace \text{TT}\rbrace, \ \lbrace \text{HH,HT}\rbrace, \lbrace \text{HH,TH}\rbrace, \lbrace \text{HH,TT}\rbrace,\lbrace \text{HT,TH}\rbrace, \lbrace \text{HT,TT}\rbrace, \lbrace \text{TH,TT}\rbrace, \ \lbrace \text{HH,HT,TH}\rbrace, \lbrace \text{HH,HT,TT}\rbrace, \lbrace \text{HT,TH,TT}\rbrace, \lbrace \text{HH,TH,TT}\rbrace \ \rbrace \end{equation}. $$
此时,除了没扔硬币和第一次扔硬币的信息以外,我们可以从 $S_2(\omega)$ 获取了更多关于 $\omega$ 的信息,并对它们进行更精细的分类。
观察上述的事件域 $\mathcal{F_0}, \mathcal{F_1}, \mathcal{F_2}$ ,不难看出,在每个事件域中,我们都可以找到对应的分类,并将所观察到的随机试验的结果及其背后根本的样本路径归入这个类别里。比如,当 $S_0=4$ 时,我们知道 $\omega \in \Omega$ ;当 $S_1=8$ 时,我们不仅知道 $\omega \in \Omega$ ,还能知道更准确的信息,即 $\omega \in \lbrace{HH,HT\rbrace} \subseteq \Omega$ ;当 $S_2=16$ 时,我们便能知道更准确的信息,即 $\omega \in \lbrace{HH\rbrace}\subseteq \lbrace{HH,HT\rbrace} \subseteq \Omega$ 。
不难看出,随着时间的推移(体现在脚标的数值不断增大), $\mathcal{F_T}$ 所包含的元素越来越多,其中的分类也越来越多,我们也越能确定 $\omega$ 究竟是什么什么样的。那么,一种很自然的想法是,如何刻画这种「随着时间不断增加的信息」。为此,我们便以 Shreve 书中对 filtration 的定义,结束这一小节:

对上例的修正
看到这里,似乎一切都大功告成了。我们通过一个例子,了解了事件域如何表示信息,并获得了 filtration 的定义。
然而,这个回答并不能这样结束,因为其中还有个很大的问题。
回到上一节中的 $\mathcal{F_2}$ ,我们会发现,这里的事件域超出了随机变量 $S$ 所能提供的信息范围。如果我们仔细回顾 $S(\omega)$ 的定义,会发现 $S_2(HT)=S_2(TH)$ 。也就是说,我们无法根据 $S_2=4$ 来判断 $\omega$ 究竟是 $TH$ 还是 $HT$ ——我们只能说, $\omega \in \lbrace{TH,HT\rbrace}$ 。

因此,如果我们真的想表示 $S_2$ 所能提供的信息,那么需要进行一些调整。将随机变量生成的 sigma 代数定义为:
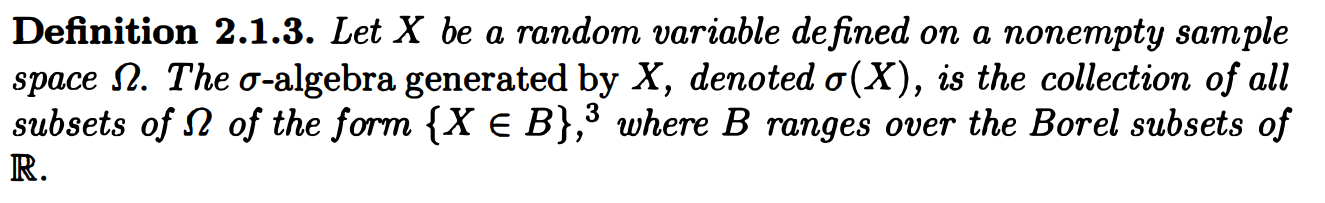
方便起见,将 $A_{HH}$ 表示以 $A_{HH}, A_{HT}, A_{TH}, A_{TT}$ 分别表示 以开头的序列 $\lbrace{以 HH 开头的序列\rbrace},$ 以开头的序列 $\lbrace{以 HT 开头的序列\rbrace},$ 以开头的序列 $\lbrace{以 TH 开头的序列\rbrace},$ 以开头的序列 $\lbrace{以 TT开头的序列\rbrace}$ 。可推得:
是一个集合,由以及这些集合的并集和余集组成。$\sigma(S_2)$是一个集合, which 由 $\varnothing, \Omega, A_{HH}, A_{HT}\cup A_{TH}, A_{TT}$以及这些集合的并集和余集组成。
不难看出,不光是 $\sigma(S_2)$ ,其他的 $\sigma(S_T)$ 都包含于 $\mathcal{F_T}$ ,因此我们可以说随机变量 $S$ 是 可测的 $\mathcal{F-}可测的$ 。可测的定义如下:
